ជំពូក១: ត្រីកោណមាត្រ-ត្រីកោណកែង

October 2nd, 2016

From Wikipedia:

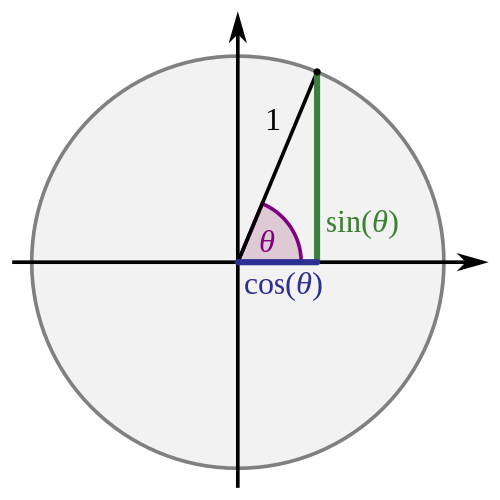
Trigonometry

Trigonometry (from Greek trigōnon, "triangle" and metron, "measure") is a branch of mathematics that studies relationships between side lengths and angles of triangles. The field emerged in the Hellenistic world during the 3rd century BC from applications of geometry to astronomical studies.[2] The Greeks focused on the calculation of chords, while mathematicians in India created the earliest-known tables of values for trigonometric ratios (also called trigonometric functions) such as sine.

ត្រីកោណមាត្រ គឺជាការសិក្សាអំពីទំនាក់ទំនងរវាង ជ្រុង និង មុំ របស់ត្រីកោណ។ ពាក្យថា "trigono-metry" គឺបានមកពីភាសាក្រិចថា trigono ($\tau\rho\acute{\iota}\gamma\omega\nu$o) ដែលមានន័យថា "ត្រីកោណ" និងពាក្យ metro ($\mu\epsilon\tau\rho\acute{\omega}$) មានន័យថា "រង្វាស់"។ ទោះបីបុព្វបុរសរបស់ជនជាតិក្រិច រួមមាន Hipparchus (អ៊ីពប៉ាគូស) និង Ptolemy (ប៉តូលេមី) បានប្រើប្រាស់ត្រីកោណមាត្រនៅក្នុងការសិក្សារបស់ពួកគេអំពីភូគព្ភសាស្ត្រនៅចន្លោះឆ្នាំ ១៥០ ម.គ. ដល់ឆ្នាំ ២០០ គ.ស. ក៏ដោយ ក៏ប្រវត្តិរបស់ត្រីកោណមាត្រនេះពិតជាមានអាយុកាលច្រើនជាងនេះទៅទៀត។ ឧទាហរណ៍ អាចារ្យម្នាក់ជនជាតិអេស៊ីបលោក Ahmes បានកត់ត្រានូវលក្ខណៈគ្រឹះនៃការគណនាត្រីកោណ មាត្រមួយចំនួន (ដែលនិយាយអំពីសមាមាត្រនៃជ្រុងរបស់ប្រាសាទពីរ៉ាមីត) ក្នុងសៀវភៅដ៏ល្បីល្បាញរបស់គាត់មានឈ្មោះថា Rhind Papyrus នៅប្រហែលឆ្នាំ ១៦៥០ ម.គ។

គេញែកត្រីកោណមាត្រចេញពីធរណីមាត្រកម្រិតងាយៗ ដោយសារតែការប្រើប្រាស់យ៉ាងទូលំទូលាយរបស់វា លើអនុគមន៍សំខាន់ៗមួយចំនួន ទាក់ទងនឹងមុំ ដែលគេស្គាល់ថាជា អនុគមន៍ត្រីកោណ មាត្រ។ មុនយើងពិភាក្សាអំពីអនុគមន៍ទាំងនោះ យើងនឹងរំឭកឡើងវិញនូវពាក្យបច្ចេកទេសសំខាន់ៗមួយ ចំនួនទាក់ទងនឹង មុំ។

១.១ មុំ

រំព្ញកអំពីនិយមន័យមួយចំនួននៅក្នុងធរណីមាត្រកម្រិតបឋមៗ គឺ៖

In elementary geometry, angles are always considered to be positive and not larger than $360^{\circ}$. For now we will only consider such angles. (Later in the text we will discuss negative angles and angles larger than $360^{\circ}$). The following definitions will be used throughout the text:

  1. Two acute angles are complementary if their sum equals \(90^{\circ}\). In other words, if \(0^{\circ} \le \angle\,A \,,\, \angle\,B \le 90^{\circ}\) then \(\angle\,A\) and \(\angle\,B\) are complementary if \(\angle\,A + \angle\,B = 90^{\circ}\).

  2. Two angles between \(0^{\circ}\) and \(180^{\circ}\) are supplementary if their sum equals \(180^{\circ}\). In other words, if \(0^{\circ} \le \angle\,A \,,\, \angle\,B \le 180^{\circ}\) then \(\angle\,A\) and \(\angle\,B\) are supplementary if \(\angle\,A + \angle\,B = 180^{\circ}\).

  3. Two angles between \(0^{\circ}\) and \(360^{\circ}\) are conjugate (or explementary) if their sum equals \(360^{\circ}\). In other words, if \(0^{\circ} \le \angle\,A \,,\, \angle\,B \le 360^{\circ}\) then \(\angle\,A\) and \(\angle\,B\) are conjugate if \(\angle\,A + \angle\,B = 360^{\circ}\).

Instead of using the angle notation \(\angle\,A\) to denote an angle, we will sometimes use just a capital letter by itself (e.g. \(A\), \(B\), \(C\)) or a lowercase variable name (e.g. \(x\), \(y\), \(t\)). It is also common to use letters (either uppercase or lowercase) from the Greek alphabet, shown in the table below, to represent angles

គេហៅអនុគម៍វ៉ិចទ័រលិបនីស គឺជាអនុគមន៍ On appelle fonction vectorielle de Leibniz l'application \(\vec{f}\) qui à tout point \(\mathrm{M}\) du plan (ou de l'espace ) associe le vecteur $\vec{f}(M)=\alpha \overrightarrow{M A}+\beta \overrightarrow{M B}+\gamma \overrightarrow{M C}$ où \(\alpha, \beta,\) y sont trois réels fixés et \(A, B, C\) trois points fixés du plan (ou de l'espace).

Propriétés : Pour tout couple de points $(M,N)$ du plan on a: \[ \vec{f}(N)-\vec{f}(M)=(\alpha+\beta+\gamma) \overrightarrow{N M} \]

Démonstration $$\begin{array}{ll} \vec{f}(N)&=&\alpha \overrightarrow{N A}+\beta \overrightarrow{N B}+\gamma \overrightarrow{N C}\\ &=& \alpha \overrightarrow{N M}+\alpha \overrightarrow{M A}+\beta \overrightarrow{N M}+\beta \overrightarrow{M B}+\gamma \overrightarrow{N M}+\gamma \overrightarrow{M C}\\ &=& (\alpha+\beta+\gamma) \overrightarrow{N M}+\alpha \overrightarrow{M A}+\beta \overrightarrow{M B}+\gamma \overrightarrow{M C}\\ &=& (\alpha+\beta+\gamma) \overrightarrow{N M}+\vec{f}(M) \end{array}$$

Barycentre de deux points

Définition 1: On appelle barycentre des points \(A\) et \(B\) ( ou \(A\) et \(B\) deux points du plan ou de I'espace ) affectés respectivement des coefficients \(\alpha, \beta\) ( ou \(\alpha, \beta\) sont des réels tels que \(\alpha+\beta \neq 0\) l'unique point \(G\) tel que \(\alpha \overrightarrow{G A}+\beta \overrightarrow{G B}=\overrightarrow{0}\)

Recent Posts